SOLUCION DE LA UNIDAD #3

Solución A

Datos

En este problema, los datos que nos dan están implícitos en la gráfica y son, precisamente, los valores de las magnitudes del movimiento armónico simple que nos piden.

Consideraciones previas

Estamos estudiando un movimiento armónico simple. Es importante recordar que la elongación de un muelle que se comporta según el movimiento armónico simple sigue una función sinusoidal cuya expresión viene dada en su forma de coseno por: x=A⋅cos(ω⋅t+φ0) m. De lo que se trata es de identificar, a partir de los valores de la gráfica, proporcionados en unidades del sistema internacional metros y segundos, las magnitudes del m.a.s. A, ω, f, T y φ0 .

Resolución

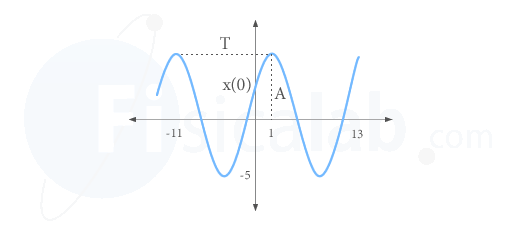
• Amplitud máxima A: Viene determinado por el valor máximo (y mínimo) entre los que oscila la gráfica, ya que, redordamos, el valor máximo que alcanza la función coseno es 1. Al multiplicarla por A, se consigue que la función oscile entre -A y A. Por tanto: A = 5 m
• El periodo T: Viene determinado por el tiempo transcurrido entre dos puntos en los que el cuerpo se encuentra en idéntico estado de vibración. En la gráfica, podemos determinarlo a partir de, por ejemplo, dos máximos consecutivos, aunque podríamos considerar dos mínimos consecutivos, dos cortes con el eje x en sentido decreciente consecutivos, etc. T = tmax2 - tmax1 = 13 - 1 = 12 s
• La frecuencia f: Podemos calcularla como la inversa del periodo: f = 1 / T = 1/12 = 0.083 Hz
• La frecuencia angular ω: Podemos calcularla a partir de la frecuencia como ω=2⋅π⋅f=0.523 rad/s 
• La fase inicial φ0 : Viene determinado por el valor de la elongación en t = 0 (aproximadamente x(0) = 2.5 m). x=A⋅cos(ω⋅t+φ0)=Acos(φ0)⇒cos(φ0)=x/A⇒φ0=cos−1(x/A)=1.047 rad 

Finalmente, en la figura siguiente pueden observarse las magnitudes señaladas:

Solución B

Datos

• Longitud del péndulo l = 70 cm = 0.7 m
• Ángulo máximo  α = 6º =  0.104 rad

Consideraciones previas

Sabemos que el péndulo se comporta como oscilador armónico cuando la amplitud de las oscilaciones es pequeña. Desde un punto de vista matemático, esta aproximación se puede hacer siempre que sin( α ) ≃ α (expresando el ángulo en radianes) y esto sucede cuando α < 20º (aproximadamente). Por tanto, el péndulo se comporta como un oscilador armónico.

Resolucion

Comenzamos representando la situación:

Aplicando trigonometría obtenemos la amplitud de las oscilaciones:

A=x ; sin(α)=xl⇒α=xl⇒x=α⋅l=0.104⋅0.7=0.0728 m

 

En cuanto a las fuerzas,  

• Valor del peso P = m·g = 0.8·9.8 = 7.84 N
• Valor de la componente normal del peso Pn = T = P·cos(α) = 7.79 N
• Valor de la componente tangencial Pt =  P·sin(α) = 0.81 N 

Y en cuanto a los sentidos de las mismas, los indicados en la figura en el caso de que el péndulo se desplace hacia la izquierda y los contrarios (en el eje tangencial) en el caso de que se desplace hacia la derecha.

Solución C

1. Falso. Cada dos segundos el cuerpo pasa por la posición de equilibrio pero en una ocasión lo hace en un sentido la siguiente vez en otro, por tanto el estado de vibración no es el mismo
2. Verdadero
3. Falso. La amplitud del movimiento es la máxima distancia que se desplaza el cuerpo respecto a la posición de equilibrio. Es decir, 3 m
4. Verdadero. f = 1/T
5. Falso. La expresión de la elongación es correcta pero fallan las unidades. En la gráfica son metros por lo tanto la correcta sería x=3⋅sin(π2⋅t) m 

Solución

Datos

• La ecuación de la elongación, que marca la posición del cuerpo en cada instante, contiene los siguientes datos:
  • A = 0.5 m
  • ω = 0.35⋅π rad/s 
  • φ0=π/4 rad

Consideraciones previas

Para obtener las ecucación de la velocidad derivamos la ecuación de la posición respecto al tiempo. 

Para obtener la ecuación de la aceleración derivamos la ecuación de la velocidad respecto al tiempo.

Resolución

v=dxdt=0.5⋅0.35⋅π⋅cos(0.35⋅π⋅t+π/4) m/s

 

a=dvdt=−0.5⋅(0.35⋅π)2⋅sin(0.35⋅π⋅t+π/4) m/s

Dando valores a las ecuaciones anteriores, por ejemplo cada T/8, obtenemos las siguientes gráficas: